고정 헤더 영역
상세 컨텐츠
본문
Number of Provinces - LeetCode
주어진 도시들 중 일부는 연결되어 있고, 일부는 연결되어 있지 않습니다. 만약 도시 A가 도시 B와 직접 연결되어 있고, 도시 B가 도시 C와 직접 연결되어 있다면, 도시 A는 간접적으로 도시 C와 연결되어 있습니다.
도성(Province)은 직접 또는 간접적으로 연결된 도시들의 그룹이며, 이 그룹 외에 다른 도시가 없는 그룹입니다.
이차원 행렬 isConnected가 주어집니다. 여기서 isConnected[i][j]는 i번 도시와 j번 도시가 직접 연결되어 있으면 1이고, 그렇지 않으면 0입니다.
전체 도성(Province)의 총 개수를 반환하세요.
There are n cities. Some of them are connected, while some are not. If city a is connected directly with city b, and city b is connected directly with city c, then city a is connected indirectly with city c.
A province is a group of directly or indirectly connected cities and no other cities outside of the group.
You are given an n x n matrix isConnected where isConnected[i][j] = 1 if the ith city and the jth city are directly connected, and isConnected[i][j] = 0 otherwise.
Return the total number of provinces.
Example 1:
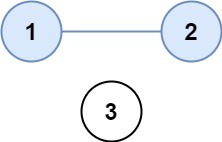
Input: isConnected = [[1,1,0],[1,1,0],[0,0,1]]
Output: 2
Example 2:
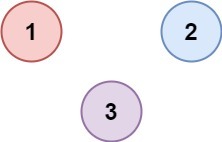
Input: isConnected = [[1,0,0],[0,1,0],[0,0,1]]
Output: 3
문제 요약:
주어진 도시들과 연결 정보를 나타내는 이차원 행렬 isConnected가 주어집니다. 이 행렬에서 1은 두 도시가 연결되어 있음을 나타내고, 0은 연결되어 있지 않음을 나타냅니다. 모든 도성(Province)의 총 수를 찾아 반환해야 합니다. 여기서 도성은 연결된 도시들의 그룹을 의미하며, 간접적으로 연결된 도시도 하나의 그룹으로 취급합니다.
풀이과정:
이 문제를 해결하기 위해 연결된 도시들의 그룹을 찾는 그래프 탐색(DFS 또는 BFS)을 사용합니다. 모든 도시를 방문하며, 방문하지 않은 도시를 찾아 그 도시와 연결된 모든 도시를 찾아내어 하나의 도성 그룹으로 취급합니다. 모든 도시를 다 돌며 도성 그룹을 찾으면, 도성(Province)의 총 개수를 세고 반환합니다.
class Solution {
public int findCircleNum(int[][] isConnected) {
int totalCnt = isConnected.length;
boolean[] visited = new boolean[totalCnt];
int retVal = 0;
for(int i = 0; i < totalCnt; i++){
if(!visited[i]){
retVal++;
dfs(isConnected, visited, i);
}
}
return retVal;
}
private void dfs(int[][] isConnected, boolean[] visited, int nowCity){
visited[nowCity] = true;
for(int i = 0; i < isConnected.length; i++){
if (isConnected[nowCity][i] == 1 && !visited[i]) {
dfs(isConnected, visited, i);
}
}
}
}
'LeetCode' 카테고리의 다른 글
| 443. String Compression (0) | 2023.10.30 |
|---|---|
| 334. Increasing Triplet Subsequence (0) | 2023.10.30 |
| 841. Keys and Rooms (0) | 2023.10.29 |
| 450. Delete Node in a BST (0) | 2023.10.29 |
| 700. Search in a Binary Search Tree (0) | 2023.10.29 |




